KAN: Kolmogorov Arnold Networks

2–3 minutes

Aug 4, 2024

In this extremely dynamic landscape of machine learning, somebody tried to reinvent ML itself giving us KANs: Kolmogorov Arnold Network. This approach challenges the conventional way of using Multi-Layer Perceptron(MLPs).

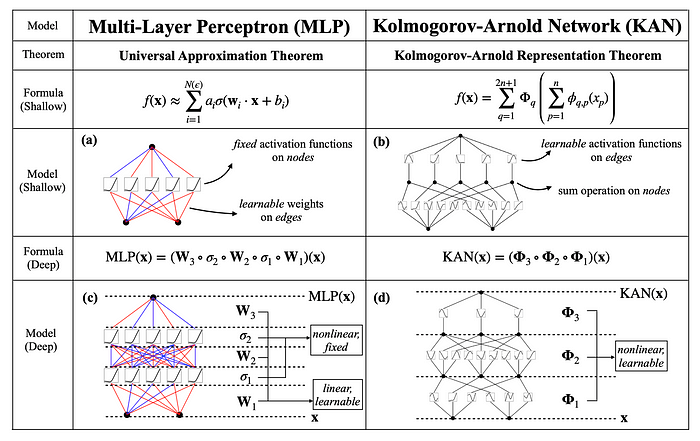
If you are reading this you probably know what do we mean by MLPs and how run training/inference on them. In theory they are extremely powerful, so much so that there is a “Universal Approximation Theorem” which tells that Neural Networks with at least one hidden layer are universal approximators. That is, it can be shown, ¹ or this intuitive explanation² from Michael Nielsen) that given any continuous function 𝑓(𝑥) and some 𝜖>0, there exists a Neural Network 𝑔(𝑥) with one hidden layer (with a reasonable choice of non-linearity, e.g. sigmoid) such that ∀𝑥,∣𝑓(𝑥)−𝑔(𝑥)∣<𝜖. In other words, the neural network can approximate any continuous function.

Similarly at the core of KANs, we have a similar theorem,

Kolmogorov-Arnold representation theorem, a mathematical theory developed by Vladimir Arnold and Andrey Kolmogorov. This theorem asserts that complex multivariate functions can be decomposed into simpler one-dimensional functions, laying the foundation for KANs’ unique structure.

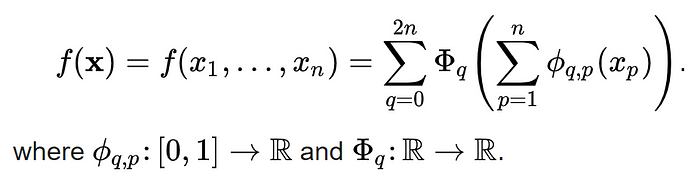
Now, The obvious question becomes what are these “simpler one-dimensional functions”. For anyone with a bit of knowledge of mathematics or computational graphics, we are talking about age old and trusted piecewise by polynomials known as Splines

Simplest Way To Understand the Working of KAN

KANs diverge from traditional MLPs by replacing fixed activation functions with learnable functions (B-Splines), along the edges of the network.

This adaptive architecture allows KANs to effectively model complex functions while maintaining interpretability and reducing the number of parameters needed.

Advantages:

Efficiency: By breaking down the function approximation into simpler univariate functions, KANs can potentially reduce the number of parameters needed.
Interpretability: The decomposition into univariate functions can make the network’s behavior more interpretable compared to traditional MLPs.
Training: Simplified structure can sometimes lead to more efficient training, especially in cases where the underlying function naturally decomposes according to the Kolmogorov-Arnold theorem.

Enhanced Scalability: KANs demonstrate superior scalability pared to MLPs, particularly in high-dimensional data scenarios.

The authors release source code for anyone to use KAN architectures for their applications. You can train your own KAN model by installing the source.

Installation via github

python -m venv pykan-env
source pykan-env/bin/activate  # On Windows use `pykan-env\Scripts\activate`
pip install git+https://github.com/KindXiaoming/pykan.git

Installation via PyPI:

python -m venv pykan-env
source pykan-env/bin/activate  # On Windows use `pykan-env\Scripts\activate`
pip install pykan

You can refer to this toy example to understand the pykan lib interface.

from kan import KAN
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
import torch
import numpy as np

dataset = {}

train_input, train_label = make_moons(n_samples=1000, shuffle=True, noise=0.1, random_state=None)

test_input, test_label = make_moons(n_samples=1000, shuffle=True, noise=0.1, random_state=None)

dataset['train_input'] = torch.from_numpy(train_input)
dataset['test_input'] = torch.from_numpy(test_input)
dataset['train_label'] = torch.from_numpy(train_label)
dataset['test_label'] = torch.from_numpy(test_label)
X = dataset['train_input']
y = dataset['train_label']

plt.scatter(X[:,0], X[:,1], c=y[:])
model = KAN(width=[2,2], grid=3, k=3)

def train_acc():
 return torch.mean((torch.argmax(model(dataset['train_input']),dim=1) ==dataset['train_label']).float())

def test_acc():
 return torch.mean((torch.argmax(model(dataset['test_input']),dim=1) == dataset['test_label']).float())

results = model.train(dataset, opt="LBFGS", steps=20, metrics=(train_acc, test_acc), loss_fn=torch.nn.CrossEntropyLoss())

Kolmogorov–Arnold Networks (KANs) represent a paradigm shift in neural network architecture. While further research and experimentation are needed to fully unlock their potential, KANs hold promise as a valuable tool for advancing machine learning and scientific discovery in the years to come.