The Sauce of the Lunar Reflectors.

Lets start with a simple optics question, the kind we had for our JEE Preparations, just a lot of them. So it goes like this, what would happen if light were to strike a system of two mirrors arranged perpendicularly to each other? How would the light behave, and where would it go after bouncing off these mirrors? This question might seem like a simple thought experiment in optics, but it paves the way to understanding one of the most ingenious and practical scientific instruments used in space exploration and physics, the lunar reflector. Think about it for some time and we shall come back to this after some time.

Original Issue, Lunar Ranging.

Lets rewind why are we even here? So far we have figured the laser travelling through the space hitting moon and coming back to earth and almost fixed face of moon due to tidal locking. The only key piece remaining in the experiment is engineering a setup which actually bounces off the incoming laser with the near perfect predictability. This article aims to do exactly the same. So shall we start?

In scientific research, especially in geophysics and astrophysics, there’s often a need to measure distances with extreme accuracy. For instance, determining the precise distance between the Earth and the Moon has profound implications for understanding gravitational effects, orbital dynamics, and even fundamental constants of nature. However, accurately measuring such vast distances poses a significant challenge: how to ensure that a signal sent from Earth can travel to the Moon and be read predictably without losing its path in the vastness of space?

The Problem.

To achieve this there was a requirement of a reflective system which can do this every time without a fail. And the most important part of all this? It must NOT require any active energy source in its operation. Were we able to device such a mechanism? Definitely, YES! It ain’t a joke for conducting lunar ranging experiments for almost five decades now.

Problem #1: The plane mirror follows the law of reflection, which states the angle of incident with normal is equal to the angle to reflection with its normal. Though its helpful, it created another major problem, the reflected ray goes into the vastness of the space, never to return. Solution? Now we know another restriction, the reflected ray must return to its source to get detected and analyzed.

Problem #2: One way of doing that is by making the incident angle zero, if we shine the laser at the exact normal of the mirror then the reflected ray shall travel back to its source. Seems like a solution, then what is the problem? Doing this is practically impossible! Think about it, how precisely you will have to place the mirrors on the moon surface that it is kept normal to an observatory at earth, also, moon has an elliptical path, which means even if we managed to pull of this feat of aligning it perfectly, this arrangement will become invalid in the next moment itself. Solution? One needs a reflective system which retraces its incident path and is also resilient to the angle of incidence.

The Solution.

So we know that a simple plane mirror is not capable of achieving what we are looking for. This seems like a perfect time to bring back our problem statement from the starting, the perpendicular 2D mirror arrangement system. Let us analyze the problem and try to trace the path of the reflected ray. This might NOT be difficult to solve if you know how to apply law of reflection. There are two observation in this problem statement.

Firstly, for a good range of incidence angle on the Mirror Y, there will be two reflections taking place, one on Mirror Y and one on Mirror X. There are going to be the cases where the incident ray reflects on Mirror Y and passes off without falling up on the Mirror X. Secondly, whenever there is reflection on the Mirror X, the angle of incidence on Mirror Y and Mirror X will be complementary to each other (i.e. the sum of the angles equal to 90 degree; i_{Mirror_Y} + i_{Mirror_X} = 90 degree) If we extrapolate on this ides then, 2 * i_{Mirror_Y} + 2 * i_{Mirror_X} = 180 degree, do you remember this from somewhere? This is exactly the condition for having two lines parallel. Finally! We have successfully devised a mechanism which solves all of our problems. Reflects back the incident ray parallelly and is independent of the incident ray.

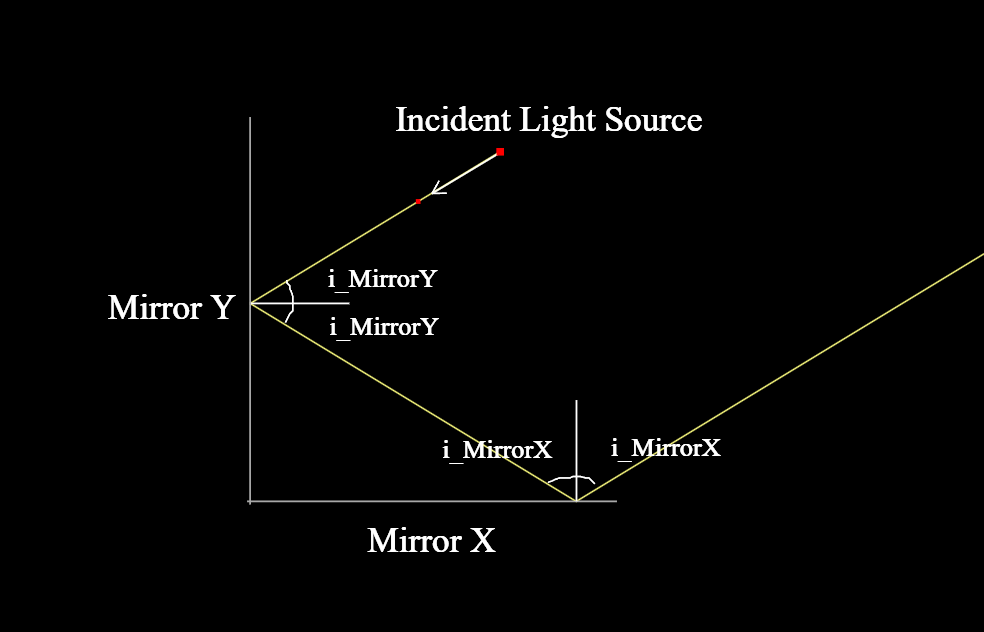
Now let us see the animation where we see the incident angle changing and the reflected ray still making it back to its incoming direction but in opposite way. Also observe after one point the ray falls off without contacting Mirror X and Mirror Y respectively.

Corner Cube in Lunar Retroreflectors.

Though this a small part of how corner cubes work, the actual retroreflectors sitting at the surface of the moon is different from this, for starters there are NO mirrors in them. Wait What?! Then why did we explaine this much about mirrors? Any Guesses? YES, you are correct, you can have reflection without reflective surfaces, and the specific phenomenon is called TIR, Total Internal Reflection. Though we don’t have mirrors, but TIR follows the rule of the reflections.

Now that I have already mentioned TIR it might not be difficult to extrapolate that the cubes are not empty but filled with optically dense transparent material with optical density, μ >= sqrt(2). Can you prove it?

Also to make it resilient in the entire spatial domain, instead of two, there are actually three perpendicular TIR surfaces, making it a true 3D Corner Cube Reflector.

Finally all the pieces of our Lunar Ranging topic came together to complete our understanding about the same. We started from an episode from Big Bang Theory to 3D Corner Cubes. Now we feel better knowing one more piece of knowledge which might come handy in other aspects of our lives. Also fun fact, you will always see your eye or camera in any 3D Corner Cube? Can you tell why? Maybe we will cover it in another article on NotRocketScience!

TL;DR.

Generated using AI.

• Optics Puzzle Introduction: Light hitting two perpendicular mirrors prompts understanding of lunar retroreflectors used in space missions.
• Lunar Ranging Need: Precise measurement of the distance between Earth and the Moon is crucial for understanding lunar dynamics.
• Problem with Traditional Reflective Systems: Traditional mirrors scatter light into space, often not returning it.
• Solution with Total Internal Reflection (TIR): Corner cube retroreflectors utilize TIR instead of traditional mirrors, requiring optically dense materials (μ ≥ sqrt(2)).
• Design Efficiency: Three perpendicular TIR surfaces ensure that light returns to its source, independent of the incident angle.
• Practical Application: From basic theoretical setups to practical applications on the Moon, showcasing how simple principles of light behavior are harnessed to solve complex problems.
• Understanding Celestial Dynamics: Enhances understanding of celestial dynamics and invites further exploration into the unique properties of 3D corner cubes.